By Steph Cornford, Senior Research Associate at the University of Bristol
I’m an ice sheet model developer, which means that most of the time it’s my role to send others to sleep. On occasion, my work garners a little attention, even if readers conclude that it’s all about bedrock typography (yes, you did read TYPography) but for the most part I talk about meshes, local refinement, linear solvers, adjoints, and so on while eyes glaze over. So I’m pleased to be able to write about an ice sheet model that I hope will grab a bit more attention. The BISICLES ice sheet model that I work on can produce some dramatic results, such as the collapse of major portions of the Antarctic Ice Sheet over just 500 years shown in the video below, but today I’m going to write about something a little more accessible.
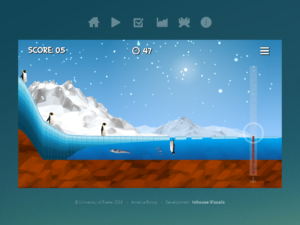
Ice Flows is an educational game aimed at school-aged students. Its development is led by Anne Le Brocq, and funded as part of a NERC large grant Ice shelves in a warming world led by Hugh Corr at the British Antarctic Survey, looking at the ice streams draining into the Filchner Ice Shelf. At first sight it looks like a game about helping penguins hunt fish, but there is a catch: you don’t interact with the penguins directly. Instead, you have to modify the shape of an ice stream and ice shelf by altering the atmosphere, bedrock and ice rheology, and the ocean. On the coarsest level, that’s exactly what the CPOM land ice model BISICLES is designed to accomplish, so Anne asked me to develop a simplified but convincing model to run inside the game.
Trying to design an ice flow model for a computer game throws up some conflicts. One one had, we wanted the model to reflect contemporary understanding well enough for students to learn about ice sheets, ice shelves, and Antarctica in particular. On the other, the game had to be playable, so that any calculations needed to be carried out quickly enough that the animation appeared smooth, and changing any of the parameters (for example, the accumulation rate) had to lead to a new steady state within seconds, to make the link between cause and effect clear.
We want students to understand that ice sheets are dynamic environments, and that processes like iceberg calving and melting near the margins are always taking place – nothing annoys a glaciologist more than a picture of a calving event presented as an undeniable proof of disaster. We want them to understand that if the accumulation of ice in the interior matches losses at the margin then an ice sheet will hold its shape, and that a change in either of these processes results in a change of shape. We need to show ice contacting submarine beds where it is thick enough, and floating on water where it is not. We will be delighted if older students can see that flow speeds up toward the margin and that mass is conserved – that downstream acceleration results in both horizontal stretching and vertical thinning. And, because it is an idea that has been so important in recent thinking, we want to include marine ice sheet instability.
There are a few things that we were confident could be left for university or later. Glen’s flow law, the Stokes equation, numerical solution of non-linear boundary value problems: these are all things that are important to ice sheet modellers, but they would slow down the calculations, and omitting them does not preclude the broad understanding outlined above. They would also have made for a longer and more expensive period of development because they are not the kind of calculations that game development tools are designed to support.
In the end, we constructed a much simplified ice sheet model that relied only on the simplest kind of calculations. The ice sheet is built up from a queue of rectangular ice blocks, which move from left to right on the screen. I’ll turn to the velocity calculation below, but for now we need only remember that it is always positive and increases from left to right smoothly. At every time-step the left and right edges of each ice block are moved according to the velocity field, which results in each block stretching (as the right edge is moving faster than the left). The height of the ice block is reduced to keep its area constant, and then reduced further if there is any ice-shelf melting to account for. After that, any ice blocks right of the screen edge are removed, and, if there is space at the left hand side of the screen, a new ice block, whose height is determined by the accumulation, is added. In other words, we implemented a simple Lagrangian scheme for mass transport.
The velocity field is recomputed at every time-step from the ice sheet shape to follow a simple curve, starting from a chosen speed at the left edge of the screen and accelerating to reach a value computed from something like the well known Schoof 2007 expression for the flux at the grounding – depending on thickness, buttressing, and rheology – at the grounding line. The strain-rate also varies from left to right, from zero at the left edge, to values derived from the calving front boundary condition beyond the grounding line. Obviously, this is a very crude approximation, but it contains the ideas we want to get across: acceleration toward the margin, the importance of buttressing, and even marine ice sheet instability.
So, if you are still awake, have a look at the Ice Flows website, where you can play an alpha version of the game already and hopefully a beta version soon.